HYPERBOLA

HYPERBOLA

A hyperbola is an open curve with two branches, the intersection of a plane with both halves of a double cone. The plane does not have to be parallel to the axis of the cone; the hyperbola will be symmetrical in an case.

Hyperbolas in the physical world: three cones of light of different widths and intensities are generated by a (roughly) downwards-pointing halogen lamp and its housing . Each cone of light intersects a nearby vertical wall in a hyperbola.

Hyperbolas produced by

interference of waves

In mathematics, a hyperbola (plural hyperbolas or hyperbolae ) is a type of smooth curve lying in a plane , defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite

bows . The hyperbola is one of the three kinds of conic section , formed by the intersection of a

plane and a double cone . (The other conic sections are the parabola and the ellipse. A

circle is a special case of an ellipse). If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

Hyperbolas arise in many ways: as the curve representing the function in the

Cartesian plane, as the path followed by the shadow of the tip of a sundial, as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of a

spacecraft during a gravity assisted swing-by of a planet or more generally any spacecraft exceeding the escape velocity of the nearest planet, as the path of a single-apparition comet (one travelling too fast ever to return to the solar system), as the scattering trajectory of a

subatomic particle (acted on by repulsive instead of attractive forces but the principle is the same), and so on.

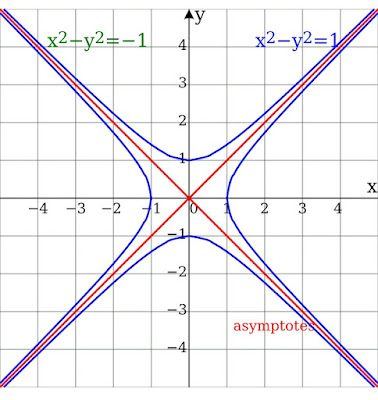
Each branch of the hyperbola has two arms which become straighter (lower curvature) further out from the center of the hyperbola. Diagonally opposite arms, one from each branch, tend in the limit to a common line, called the asymptote of those two arms. So there are two asymptotes, whose intersection is at the center of symmetry of the hyperbola, which can be thought of as the mirror point about which each branch reflects to form the other branch. In the case of the curve

the asymptotes are the two

coordinate axes.

Hyperbolas share many of the ellipses' analytical properties such as eccentricity ,

focus , and directrix . Typically the correspondence can be made with nothing more than a change of sign in some term. Many other mathematical objects have their origin in the hyperbola, such as hyperbolic paraboloids (saddle surfaces), hyperboloids ("wastebaskets"), hyperbolic geometry ( Lobachevsky's celebrated non-Euclidean geometry ), hyperbolic functions (sinh, cosh, tanh, etc.), and gyrovector spaces (a geometry proposed for use in both relativity and quantum mechanics which is not Euclidean).

Etymology and history

The word "hyperbola" derives from the Greek

ὑπερβολή, meaning "over-thrown" or "excessive", from which the English term

hyperbole also derives. Hyperbolae were discovered by Menaechmus in his investigations of the problem of doubling the cube , but were then called sections of obtuse cones. [1] The term hyperbola is believed to have been coined by Apollonius of Perga (c. 262–c. 190 BC) in his definitive work on the

conic sections , the Conics .[2] For comparison, the other two general conic sections, the ellipse and the parabola , derive from the corresponding Greek words for "deficient" and "comparable"; these terms may refer to the eccentricity of these curves, which is greater than one (hyperbola), less than one (ellipse) and exactly one (parabola).

Comparison with circular functions

Circle and hyperbola tangent at (1,1) display geometry of circular functions in terms of circular sector area u and hyperbolic functions depending on

hyperbolic sector area u .

The hyperbolic functions represent an expansion of trigonometry beyond the circular functions . Both types depend on an argument , either circular angle or hyperbolic angle .

Since the area of a circular sector with radius r and angle u is   

it will be equal to u when r = square root of 2 . In the diagram such a circle is tangent to the hyperbola xy = 1 at (1,1). The yellow sector depicts an area and angle magnitude. Similarly, the yellow and red sectors together depict an area and hyperbolic angle magnitude.

The legs of the two right triangles with hypotenuse on the ray defining the angles are of length √2 times the circular and hyperbolic functions.

Mellon Haskell of University of California, Berkeley described the basis of hyperbolic functions in areas of hyperbolic sectors in an 1895 article in Bulletin of the American Mathematical Society (see External links). He refers to the hyperbolic angle as an invariant measure with respect to the squeeze mapping just as circular angle is invariant under rotation.

Identities

The hyperbolic functions satisfy many identities, all of them similar in form to the

trigonometric identities . In fact, Osborn's rule

[16] states that one can convert any trigonometric identity into a hyperbolic identity by expanding it completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching the sign of every term which contains a product of 2, 6, 10, 14, ... sinhs. This yields for example for the addition theorem  .

The derivative of sinh x is cosh x and the derivative of cosh x is sinh x ; this is similar to trigonometric functions, albeit the sign is different (i.e., the derivative of cos x is −sin x).

The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic ones that does not involve complex numbers.

The graph of the function a cosh( x /a ) is the

catenary , the curve formed by a uniform flexible chain hanging freely between two fixed points under uniform gravity.

Relationship to the exponential function

From the definitions of the hyperbolic sine and cosine, we can derive the following identities:

These expressions are analogous to the expressions for sine and cosine, based on

Euler's formula , as sums of complex exponentials.

Hyperbolic functions for complex numbers

Since the exponential function can be defined for any complex argument, we can extend the definitions of the hyperbolic functions also to complex arguments. The functions sinh z and cosh z are then holomorphic.

Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers:

Thus, hyperbolic functions are periodic with respect to the imaginary component, with period ( for hyperbolic tangent and cotangent).

Hyperbolic functions in the complex plane

The hyperbolic functions are--

where i is the imaginary unit with the property that i 2 = −1.

The complex forms in the definitions above derive from Euler's formula .

Special meanings

Hyperbolic cosine

It can be shown that the area under the curve of cosh ( x ) over a finite interval is always equal to the arc length corresponding to that interval:

Standard analytic expressions

sinh , cosh and tanh

csch, sech and coth

(a) cosh( x ) is the

average of e x and e −x

(b) sinh( x) is half the

difference of e x and e

HYPERBOLIC FUNCTIONS

HYPERBOLIC FUNCTIONS

A ray through the unit hyperbola in the point , where is twice the area between the ray, the hyperbola, and the -axis. For points on the hyperbola below the -axis, the area is considered negative (see

animated version with comparison with the trigonometric (circular) functions).

In mathematics, hyperbolic functions are analogs of the ordinary trigonometric , or circular functions.

The basic hyperbolic functions are the

hyperbolic sine "sinh" (/ ˈsɪntʃ/ or / ˈʃaɪn/ ), [1] and the hyperbolic cosine "cosh" (/ ˈkɒʃ/ ),[2] from which are derived the hyperbolic tangent "tanh" ( / ˈtæntʃ/ or /ˈθæn/ ), [3] hyperbolic cosecant "csch" or "cosech" (/ ˈkoʊʃɛk/ [2] or /

ˈkoʊsɛtʃ/ ), hyperbolic secant "sech" ( /ˈʃɛk/ or

/ ˈsɛtʃ/ ),[4] and hyperbolic cotangent "coth" (/

ˈkoʊθ/ or / ˈkɒθ/ ), [5][6] corresponding to the derived trigonometric functions.

The inverse hyperbolic functions are the area hyperbolic sine "arsinh" (also called "asinh" or sometimes "arcsinh") [7][8] and so on.

Just as the points (cos t , sin t ) form a circle with a unit radius, the points (cosh t , sinh t ) form the right half of the equilateral hyperbola. The hyperbolic functions take a real argument called a hyperbolic angle. The size of a hyperbolic angle is twice the area of its

hyperbolic sector . The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.

Hyperbolic functions occur in the solutions of many linear differential equations , for example the equation defining a catenary , of some cubic equations , in calculations of angles and distances in hyperbolic geometry and of

Laplace's equation in Cartesian coordinates.

Laplace's equations are important in many areas of physics , including electromagnetic theory , heat transfer, fluid dynamics, and

special relativity .

In complex analysis , the hyperbolic functions arise as the imaginary parts of sine and cosine. When considered defined by a complex variable, the hyperbolic functions are rational functions of exponentials , and are hence

holomorphic.

Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and

Johann Heinrich Lambert. [9] Riccati used Sc. and Cc. ( [co]sinus circulare ) to refer to circular functions and Sh. and Ch. ( [co]sinus hyperbolico ) to refer to hyperbolic functions. Lambert adopted the names but altered the abbreviations to what they are today. [10] The abbreviations sh and ch are still used in some other languages, like French and Russian.

Since the eccentricity of a hyperbola is always greater than one, the center B must lie outside of the reciprocating circle C .

This definition implies that the hyperbola is both the locus of the poles of the tangent lines to the circle B , as well as the envelope of the polar lines of the points on B . Conversely, the circle B is the envelope of polars of points on the hyperbola, and the locus of poles of tangent lines to the hyperbola. Two tangent lines to B have no (finite) poles because they pass through the center C of the reciprocation circle

C ; the polars of the corresponding tangent points on B are the asymptotes of the hyperbola. The two branches of the hyperbola correspond to the two parts of the circle B that are separated by these tangent points.

Quadratic equation

A hyperbola can also be defined as a second-degree equation in the Cartesian coordinates (x ,

y ) in the plane,

provided that the constants A xx , A xy , A yy , B x,

B y , and C satisfy the determinant condition

This determinant is conventionally called the

discriminant of the conic section. [3]

A special case of a hyperbola—the degenerate hyperbola consisting of two intersecting lines—occurs when another determinant is zero:

This determinant Δ is sometimes called the discriminant of the conic section. [4]

Given the above general parametrization of the hyperbola in Cartesian coordinates, the eccentricity can be found using the formula in

Conic section#Eccentricity in terms of parameters of the quadratic form.

The center (x c , y c ) of the hyperbola may be determined from the formulaeformulae

In terms of new coordinates, ξ = x − x c and η =

y − yc , the defining equation of the hyperbola can be written

The principal axes of the hyperbola make an angle φ with the positive x-axis that is given by

Rotating the coordinate axes so that the x-axis is aligned with the transverse axis brings the equation into its canonical form

Mathematical definitions

A hyperbola can be defined mathematically in several equivalent ways.

Conic section

Three major types of conic sections.

A hyperbola may be defined as the curve of

intersection between a right circular conical surface and a plane that cuts through both halves of the cone. The other major types of conic sections are the ellipse and the parabola ; in these cases, the plane cuts through only one half of the double cone. If the plane passes through the central apex of the double cone a

degenerate hyperbola results — two straight lines that cross at the apex point.

Difference of distances to foci

A hyperbola may be defined equivalently as the

locus of points where the absolute value of the

difference of the distances to the two foci is a constant equal to 2 a , the distance between its two vertices. This definition accounts for many of the hyperbola's applications, such as

multilateration; this is the problem of determining position from the difference in arrival times of synchronized signals, as in GPS .

This definition may be expressed also in terms of tangent circles. The center of any circles externally tangent to two given circles lies on a hyperbola, whose foci are the centers of the given circles and where the vertex distance 2 a equals the difference in radii of the two circles. As a special case, one given circle may be a point located at one focus; since a point may be considered as a circle of zero radius, the other given circle—which is centered on the other focus—must have radius 2 a . This provides a simple technique for constructing a hyperbola, as shown below . It follows from this definition that a tangent line to the hyperbola at a point P bisects the angle formed with the two foci, i.e., the angle F 1 P F 2 . Consequently, the feet of perpendiculars drawn from each focus to such a tangent line lies on a circle of radius

a that is centered on the hyperbola's own center.

A proof that this characterization of the hyperbola is equivalent to the conic-section characterization can be done without coordinate geometry by means of Dandelin spheres .

Directrix and focus

A hyperbola can be defined as the locus of points for which the ratio of the distances to one focus and to a line (called the directrix) is a constant e that is larger than 1. This constant is the eccentricity of the hyperbola. The eccentricity equals the secant of half the angle between the asymptotes of the hyperbola, so the eccentricity of the hyperbola xy = 1 equals the square root of 2.

By symmetry a hyperbola has two directrices, which are parallel to the conjugate axis and are between it and the tangent to the hyperbola at a vertex. One directrix and its focus is enough to produce both arms of the hyperbola.

Reciprocation of a circle

The reciprocation of a circle B in a circle C always yields a conic section such as a hyperbola. The process of "reciprocation in a circle C " consists of replacing every line and point in a geometrical figure with their corresponding pole and polar, respectively. The

pole of a line is the inversion of its closest point to the circle C , whereas the polar of a point is the converse, namely, a line whose closest point to C is the inversion of the point.

The eccentricity of the conic section obtained by reciprocation is the ratio of the distances between the two circles' centers to the radius r of reciprocation circle C. If B and C represent the points at the centers of the corresponding circles, then

For example, the eccentricity of a rectangular hyperbola (θ = 45°, a = b ) equals the square root of two: e =

Every hyperbola has a conjugate hyperbola, in which the transverse and conjugate axes are exchanged without changing the asymptotes. The equation of the conjugate hyperbola of

If the graph of the conjugate hyperbola is rotated 90° to restore the east-west opening orientation (so that x becomes y and vice versa), the equation of the resulting rotated conjugate hyperbola is the same as the equation of the original hyperbola except with a and b exchanged. For example, the angle θ of the conjugate hyperbola equals 90° minus the angle of the original hyperbola. Thus, the angles in the original and conjugate hyperbolas are complementary angles, which implies that they have different eccentricities unless θ = 45° (a rectangular hyperbola). Hence, the conjugate hyperbola does not in general correspond to a 90° rotation of the original hyperbola; the two hyperbolas are generally different in shape.

A few other lengths are used to describe hyperbolas. Consider a line perpendicular to the transverse axis (i.e., parallel to the conjugate axis) that passes through one of the hyperbola's foci. The line segment connecting the two intersection points of this line with the hyperbola is known as the latus rectum and has length 

. The semi-latus rectum l is half of this length, i.e.

The focal parameter p is the distance from a focus to its corresponding directrix, and equals

A hyperbola aligned in this way is called an "East-West opening hyperbola". Likewise, a hyperbola with its transverse axis aligned with the y-axis is called a "North–South opening hyperbola" and has equation

Every hyperbola is congruent to the origin-centered East-West opening hyperbola sharing its same scale and eccentricity e (its shape, or degree of "spread"), and is also congruent to the origin-centered North–South opening hyperbola with identical scale and eccentricity e — that is, it can be rotated so that it opens in the desired direction and can be translated (rigidly moved in the plane) so that it is centered at the origin. For convenience, hyperbolas are usually analyzed in terms of their centered East-West opening form.

If is the distance from the center to either focus, then .

Here a = b = 1 giving the unit hyperbola in blue and its conjugate hyperbola in green, sharing the same red asymptotes.

The shape of a hyperbola is defined entirely by its eccentricity e , which is a dimensionless number always greater than one. The distance

c from the center to the foci equals ae . The eccentricity can also be defined as the ratio of the distances to either focus and to a corresponding line known as the directrix ; hence, the distance from the center to the directrices equals a /e . In terms of the parameters a , b , c and the angle θ, the eccentricity equals