A hyperbola aligned in this way is called an "East-West opening hyperbola". Likewise, a hyperbola with its transverse axis aligned with the y-axis is called a "North–South opening hyperbola" and has equation

Every hyperbola is congruent to the origin-centered East-West opening hyperbola sharing its same scale and eccentricity e (its shape, or degree of "spread"), and is also congruent to the origin-centered North–South opening hyperbola with identical scale and eccentricity e — that is, it can be rotated so that it opens in the desired direction and can be translated (rigidly moved in the plane) so that it is centered at the origin. For convenience, hyperbolas are usually analyzed in terms of their centered East-West opening form.

If is the distance from the center to either focus, then .

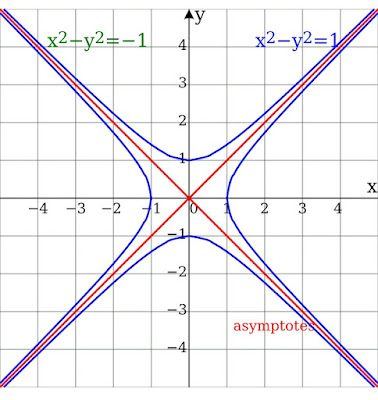
Here a = b = 1 giving the unit hyperbola in blue and its conjugate hyperbola in green, sharing the same red asymptotes.

The shape of a hyperbola is defined entirely by its eccentricity e , which is a dimensionless number always greater than one. The distance

c from the center to the foci equals ae . The eccentricity can also be defined as the ratio of the distances to either focus and to a corresponding line known as the directrix ; hence, the distance from the center to the directrices equals a /e . In terms of the parameters a , b , c and the angle θ, the eccentricity equals